Читальный зал -->  Цилиндрические электромагнитные экраны 

1 2 [ 3 ] 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

т. д. в пространстве V(a) [см. (5.51)].

Дифференциальные уравнения лоля. Решения (1.3) -(1.9) основываются а преобразовании их к форме, в которой сохраняется только одна из величин Н или Е. Для изотропных (\lx=\.y=\lz= , 8*= = 8v=8z=8; 7х=7у=Тг=Т и линейных сред (n=const; e=const; 7=const) первое уравнение Максвелла (1.3) можно путем подстановки (1.4) преобразовать к форме

го1го1Я= (Y + s--jrot£ =

Учитывая тождественность векторной операции rot rot Д= = graddivff-кн, а также отсутствие источников в линии поля 01.5), получаем дифференциальное уравнение в частных производных, описывающее магнитное поле в неидеальном диэлектрике,

v= Tf(1.10)

Аналогично можно получить уравнение для напряженности электрического поля при отсутствий свободных зарядов (divZ) = 0)

Для синусоидального поля Я = У :Я =1Я 1е*я;

и (1.10) и (Ы 1) принимают вид уЯ = ПЯ,; АЕ = ГЕ (1.116)

причем Г=>/(вц.(у-+- /<ое) =а + +УР, где Г - постоянная распрост-ранення; а--постоян!рая затухания; Р - фазовая постоянная.

Для металлических сред Гмет=

= а; амет = Рмет = .

В линейных средах для проводников плотностью токов смещения dD/dt можно пренебречь по сравнению с плотностью токов проводимости и тогда (1.10) н (1.11) 16

(I.IIa)

для n=const и 8=const приобретают форму

rH==VidHldt-; yjEiu-idEjdl. (1.12)

Уравнения (1.12) описывают одновременно диффузию поля в проводнике в динамических режимах, поэтому их также называют диффузионными уравнениями.

Для синусоидального поля (1.11а) уравнение (ilJ12) принимает вид

у=Я = аЯ ; Е =аЕ . (1.13)

причем

а = >/<от = (1+/) = 1

(1.14)

Решение (1.13) для плоской поляризованной волш, характеризуемой формулами

ту - тг ~ 0; =

dHJdK=dHJdy=Q\

принимает вид Я = Л.е + Л,е-

[1.15)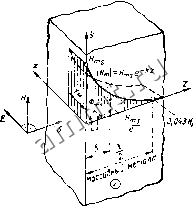

Диэлектрик ©

Рис. 1.3. Проникновение плоской волны r металлическое пространство

Внутри металлического полупространства (рис. 1.3) напряженность поля Н (z->-оо)фоо, тогда решение (1.Г5) принимает вид (см. [1.22])

(1.16)

У = аЯ ,е- . Поток на единицу длины, Вб/м,

(1.17)

а также

Мощность. В-А, внутри металла определяется из теоремы Пойнтинга

/;=Sda или P, = P + /Q =

= §Suu. (1.19)

причем для синусоидальной плоской волны Ёектор Пойнтинга

= (14-ЛУ f-е-*-. (1.20)

При 2=0 вектор представляет плотность полной мощности, В А/м*, поступающей в полупространство,

5e = P, + /Q. = (I+/)/S

(1.21)

Эквивалентная глубина проникновения, на которой амплитуда поля Нт уменьшается в е раз.

(1.22)

Эта величина представляет собой толщину эквивалентного по-

верхностного слоя массивного металлического полупространства, которое для постоянного тока представляет собой Такое же сопротивление Ru кЁкое представляет полу-простраество для переменного тока вследствие поверхностного эффекта.

Максимальное значение тока /ml в полупрострайстве, приходящееся на 1 м длины, называемое в электрических машинах линейной нагрузкой Am или поверхностной линейной плотностью тпов тока, аналогично (1.17)

/ - а /

mi - m - т пов -

z=J J- d2= = (l-/):

I /.J = I = I / пов I =8-

Таким образом, можно считать, что в слое б плотность тока постоянна и ее максимальное значение 1 ,

составляет =

Аналогично можно рассчитывать величину Rf,i металлического полупространства для единичного потока Фщ! (1-17), а также поток

Фт11=р;=8, принимая, что индукция в слое б постоянна и составляет р==. Bms.

Комплексное единичное магнитное ч;опротивление, Гн (на I м длины вдоль оси хну, ом. рис. 1.3), для потока Ф! имеет вид

(I.23>

где означает магнитное сопротивление материала; Rib обусловлено реакцией вихревых токов.

Единичное сопротивление, Ом,

для тока /ml

1+ /

(1.24)

Полное сопротивление Zi представляет одновременно полное волновое сопротивление, которое описывается уравнением

Для меди при 50 Гц волновое сопротивление (Zcu = 2,7 IQ- Ом, для стали с проницаемостью Цг>

>1200 ZFe>I00 Zcu.

Длина волны в металле Х = = 2Ь= 2l/I= 2 l/.

(1.26)

Скорость волиы в металле

А Г HY > MY

(1.27)

Диэлектрики. Для диэлектриков (y=0) из (II.10) и (il.lil) получаем волновые уравнения

Н=±;Е = ±, (1.28)

ц2 2

Ц2

при ЭТОМ скорости волны в диэлектрике и воздухе соответственно равны

v=\jV; v = c = l/Vi (1.29)

где с=3-10* м/с; цо=4я-10- Гн/м; 60=8,854-10-12 Ф/М.

Полное волновое сопротивление в диэлектрике

; отр

(1.30)

для воздуха Zbo3 = К / s = = 377 Ом, для трансформаторного масла /мас= 243 Ом (1.31)

Длина волны в воздухе при /= =50 Гц составляет

Л5 = с = 6000 км.

(1.32)

Векторный потенциал. Все виды полей можно исследовать с помощью магнитного векторного потенциала, который определяется как

В = rot А. (1.33)

Тогда для мгновенных синусоидальных значений

E:=:-dA/dt-gTadV; ) (1.34)

= - hArn.

поскольку rot£=-rot (ЭЛ/(Э= = -rot {dA/dt + gradV); rot grad V=0.

Принимая во внимание условие divAi=0, получаем

AA = -iiJ(J = -E); (1.35)

AA=i>.-dA/dt или ДЛ =а=Л-/,

(1.36)

а также

CJdV

47С J г

(1.37)

где / ст-плотность стороннего тока; г - расстояние от элемента dV проводника с током до точки, в которой определяется векторный потенциал А.

1.2.2. Уравнения электродинамики для медленно движущихся сред (у<Сс). Если система координат, связанная с наблюдателем, расположена таким образом, что происходит относительное движение исследуемого тела со скоростью v относительно исходной системы координат (рис. 11.4), то в каждой точке {х, у, z) внутри исследуемого тела индукция D или В будет функцией координат X, у, z этой точки, а также времени t.

Для электрического поля (рис. 1.4,а) в правой части уравнения (1.8) находится величина Z)==

1 2 [ 3 ] 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.