Читальный зал -->  Цилиндрические электромагнитные экраны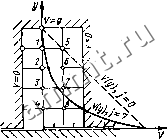 

1 2 3 4 5 6 7 [ 8 ] 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

Рис. 1.15. Определение магнитного потенциала в пазу электрической машины по осн у методом итераций (см. табл. 1.3)

рнческой машины по осн у (рис. 1.15).

Решение. Принимаем произвольно (табл. 1.3) в качестве нулевого приближения, что потенциалы в точках 1, 2, 3,4 равняются номерам этих точек, а точки 5-8 вследствие симметрии имеют такие же значения. Для первой нтерацин по (1.81) получаем

1+0 + 0 + 2

2+1+0+3

3+2+0+4

= 0,75 = 1/5; : 1,5 = Ив; = 2,25 = V,; V, =

= 4,25 = v8.

Последующие величины рассчитываем на основе предыдущих итераций по выражению

(1.88)

до получения точности АО) - /4()<0,04. Таблица 1.3. Расчет магнитного потенциала

Метод релаксации и подрелак-сации. Процесс итерации можно существенно ускорить, если вместо среднего значения соседних узлов Ast, рассчитанного по (1.81), в узел (i, к) подставим величину

ЛГ = Л4>-Ьг(Л5г-Л14) или

Д(> = Л<У-}-г(Л>-ЛК>), (1.89)

где г - коэффициент релаксации.

Простейший метод релаксации [1.4] при г=1 идентичен описанному методу итераций. Соответствующим выбором г>1, обычно 1г= = 1,1-5-1,3 [1.18], получаем так называемый метод подрелаксации, применением которого можно ускорить уменьшение ошибки. Однако точность выбора нулевого приближения в первом методе играет более важное значение.

Метод прогона. Более быстрым методом решения разностных систем по сравнению с методом итераций считается метод прогона с использованием так называемой неявной схемы [1.16]. Например, одномерное уравнение Пуассона dV/dx = p(x) можно в соответствии с (1.77) для k-w. строки представить в виде

Ау, ,-С,У, + В.у,,=

= -f,., i = l. 2,..., iV-1 (1.90)

с граничными условиями

(1.91)

где Аи Ей Си ри qu Р2, 92 - заданные параметры; N - число ячеек

V.jj+) в пазу методом итераций

Номер итерации								v>
	0,75	1,50	2,25	4,25	0,75	1,50	2,25	4,25
	0,56	1,13	2,00	4.13	0,56	1,13	2,00	4,13
	0,42	0,92	1.82	4,03	0.42	0,92	1,82	4,03
	0,34	0,79	1,69	3,96	0,34	0,79	1,69	3,96
	0,28	0,71	1,61	3,91	0,28	0,71	1,61	3,91
	0,25	0,65	1,56	3,88	0,25	0,65	1,56	3,88
	0,23	0,62	1,52	3,86	0,23	0,62	1,52	3,86

исследуемой области вдоль оси х (см. рис. 1.13).

Решение (1.90) ищется в форме

= + i = 0, 1. 2....

.... N -I. (1.92)

где fli+i, bi+i - неизвестные пока коэффициенты прогона.

Используя (1.92) в качестве рекуррентного выражения

= fl,.fl,., + аЛч-. + 6,- (1.93)

и подставляя (1.93) и (1.92) в (1.90), получаем

K+,(a,-C,-) + /]V.4..+

+ [(а,Л.- - Сд + Afi, + f,] = 0.

(1.94)

Из (1.94) следует, что (1.90) будет выполняться при условии, что каждое из выражений в квадратных скобках уравнения (1.94) равняется нулю. Отсюда получаются рекуррентные формулы для коэффициентов прогона

(1.95)

Граничные величины a и 6 определяются при приравнивании (1.92) для условия t=0 к (1.91), откуда

а. = Л; Ь, = р,. (1.96)

Величина Vn, необходимая для начала расчетов по (1,92), определяется подстановкой (1.92) прие= =N-\ в (1.91), откуда

Выражения (1.92), (1.95) -(1.97) определяют алгоритм решения (см. рис. 1.14) граничного уравнения (1.90), (1.91). Последовательность действий при так называемых правых прогонах заключается в следующем:

получение входных данных (граничные условия, сетка);

расчет а, Ь по (1.96);

расчет Ci+i, по (1.95), начиная от 02, и перемещаясь от левой границы к правой (прямой прогон); 32

расчет Vn по (1.97);

расчет узловых функций Vi по (1.92), начиная от V i и перемещаясь от правой границы к левой (обратный прогон).

Существуют аналогичные выражения для левых прогонов.

Условия стабильности прогона по [1.16]:

Л,>0; В,>0; Л, + ,;

0</7<1 {а = \, 2). (1.98)

Смешанный метод решения многомерных задач. В многомерных задачах используется соединение итерационного метода с методом прогона. Например, уравнение проводимости (1.12) дН dt

. -V

ff\s = 9{K. у. t); Н{к. у. 0) = Н,{к, у) (1.99)

представляем, в соответствии с [1.16] в разностной форме

0,5т

-{-ДЯС-М, (1.100)

где А=Ах-\-Ау - разностный оператор, причем Ах=д/дх; Ау= =52/5 /2; и,-л-t-1 - временные диапазоны сетки с шагом интегрирования т.

После некоторых преобразований (1.100) принимает форму, соответствующую методу прогона,

+ -1-ЯГ/Л> = --,;г = 1,2....

i = 0, (1.101)

Я<Г,>-2(± + )я -> +

mi=~Fk ft=i. 2...

k = Q),N,. (1.102)

Если известно Я=Я >, то рассчитываем F, затем методом прогона вдоль строк k=\,. 2, Л2-1 решаем (1.101), определяя + 5 во всех узлах сетки. Затем рассчитываем F и решаем (1.102) вдоль столбцов 1=1, 2, N\ - \, определяя Я( + . При переходе от слоя n-f 1 к слою п-\-2 процедура повторяется.

Метод линий. К смешанным методам относится метод линий [1.29, 1.37], который основывается на том, что в решаемом дифференциальном уравнении остаются производные от одной независимой переменной, а производные от остальных независимых переменных заменяются произведениями конечных разностей. В двумерных системах это соответствует разделению поля на п параллельных слоев. В зоне каждого слоя действует обычное дифференциальное уравнение. Для всего пространства, занятого полем, в результате получается система п обычных уравнений.

Метод Колорадо [1.37, 1.38]. Этот метод основан на численном решении нелинейного уравнения Пуассона для магнитного векторного потенциала. При этом учитывается переменная проницаемость стали. После разностных преобразований дифференциального уравнения получается система нелинейных алгебраических уравнений, которая затем решается итерационным методом подрелаксации. В результате решения определяются значения векторного потенциала во всех дискретных точках исследуемого пространства с плоским стационарным или квазистацконарным магнитным полем, возбуждаемым током с известной плотностью J.

1.4.2, Метод Монте-Карло. Данный метод основан на получении потенциала V в произвольном узле сетки (см. рис. 1.13,6) при условии, что известны граничные значения V(Ui, Vi) в узловых точках (щ, Vi) граничной линии С, окружающей выделенную область потенциального поля.

После выхода из узла (д; Ух) (рис. 1.13,6) движение происходит вдоль линии сетки шагами, выбираемыми случайно после каждого перемещения среди четырех значений ±Ал:, ±А /. После достижения произвольного граничного узла операция повторяется. При очень большом числе повторений перемещение заканчивается п\ раз в граничной точке ( 1, vi), П2 раз - в точке ( 2, Уг), Hi раз - в точке {Ui,Vi), причем П1+Я2+ ... =N.

Вероятность того, что, выходя из точки (х, у) по случайной траектории, попадем в точку {щ, у<), составляет

Р{х, у, ui, Vi) = nijN. (1.103)

Среднее значение потенциала V{u, у)* на конце случайной траектории, начинающейся в точке (д:, у), определяется [1.13] как

V(u,vY-y = l-[n,V(u v,) +

-{-n,V{u v,)-}-...-ny{ui. vi)]

2Р{>с. у. Ui.V:)V{u Vt) (1.104)

и равняется потенциалу в рассматриваемой начальной точке

V{K, y)V{u, vy-y. (1.105)

Вероятность (1.103) удовлетворяет приближенное разностное уравнение Лапласа (1.81). Метод Монте-Карло не совсем точен и требует большого времени на проведение расчетов и применения генератора случайных чисел. Однако этот метод применим для приближенных качественной и количественной оценок сложных процессов [1.5].

1.4.3. Метод интегральных уравнений. В экстремальных задачах электродинамики проводящих сред часто неизвестны условия на границе исследуемого тела, поскольку их конечное описание зависит от реакции среды на известное первичное возбуждающее поле. Классическим примером этого является реакция вихревых токов, индуктированных в сечении массивных по-

1 2 3 4 5 6 7 [ 8 ] 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.