
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
|
Читальный зал --> Полупроводниковая схемотехнология ВОЗМОЖНОСТЬЮ получения импульсов Дирака. Необходимо, как это иллюстрируется рис. 22.3, формировать импульсы с конечными значениями амплитуды и конечной длительностью, т.е. в этом случае не будет выполняться условие предельного перехода (22.2). Подставляя выражение (22.2) в (22.1), получаем для конечного е приближенную импульсную последовательность uAt)= i; t/i(gr,(t-g. (22.5) Применяя преобразование Фурье, находим спектр sinner/ . Это тот же спектр, что и для импульсов Дирака, однако с наложением весовой функции, вйеденной для ослабления высокочастотных составляющих. Особенно интересен случай ступенчатой функции. Для нее длительность импульса 8 7 равна длительности выборки Та. Отсюда получаем спектр (22.7) Весовая функция на рис. 22.5 представлена символическим спектром импульсов Дирака. При частоте выборки 0,5/ имеет место ослабление сигнала с коэффициентом 0,64; при частоте выборки 0,2f ослабление составляет 0,94. Таким образом, искажения спектра до частоты среза /мс остаются пренебрежимо малыми, если выбрать fa ~ 5/макс- Для восстановления первоначального сигнала необходим, как показано выше, фильтр нижних частот, который отфильтровывает спектральные составляющие с частотой ниже Реальный фильтр имеет спад коэффициента усиления конечной крутизны. Чтобы разделить спектральные составляющие, нужно выбрать частоту fa также больше 2/макс- Тогда можно добиться того, что на нижней частоте fa - /макс ослабление будет достаточно большим. В этой связи даже целесообразно вместо последовательности импульсов Дирака применить ступенчатую функцию, так как соответствующая весовая функция имеет характер фильтра нижних частот. Искажения спектра в полосе пропускания можно устранить, несколько увеличив коэффициент усиления фильтра нижних частот вблизи частоты среза. Для того чтобы на частотах выше /макс добиться достаточного снижения коэффициента усиления, можно рекомендовать выбрать нулевую точку частотной характеристики вблизи частоты/, -/макс 22.2. ЦИФРОВАЯ ФУНКЦИЯ ПЕРЕДАЧИ ФИЛЬТРА В гл. 13 мы видели, что аналоговые фильтры реализуются на основе интеграторов, сумматоров и элементов, задающих значения масштабных коэффициентов. Переход к цифровым фильтрам производится путем замены интегратора элементом задержки. Такой элемент задержки можно построить, например, на основе регистра сдвига, в котором выбранное значение входной функции сдвигается с частотой выборки fa. в простейшем случае задержка осуществляется на один временной интервал 7. Пример такого цифрово-  ; Весовая щнкция Рис. 22.5. Преобразование спектра последовательности Дирака в спектр ступенчатой функции с помощью весовой функции I (sin nflQKnflfa) I. {у Им)) Рис. 22.6. Пример цифрового фильтра первого порядка. го фильтра первого порядка представлен на рис. 22.6. Рассмотрим его режим работы во временной области. 22.2.1. ОПИСАНИЕ ВО ВРЕМЕННОЙ ОБЛАСТИ Пусть задана временная последовательность {x(tj,)}, которая служит в качестве входного сигнала для устройства, показанного на рис. 22.6. Найдем соответствующую выходную последовательность {yit)}. В момент времени на входе памяти находится числовое значение x(t) - Соу(1ц). Со сдвигом на один такт оно появляется на выходе устройства памяти. При этом для выходной последовательности имеем соотнощение yiti) = x(g - Соу{д. (22.8) Это дифференциальное уравнение подобно дифференциальному уравнению для аналоговой системы. Задавая начальное значение у (to), его можно использовать в качестве рекуррентной формулы для вычисления выходной последовательности. В качестве примера выберем у (to) = О и найдем переходную характеристику для Со = - 0,75. Она приведена на рис. 22.7. Понятно, что схема является фильтром нижних частот. 22.2.2. ОПИСАНИЕ В ЧАСТОТНОЙ ОБЛАСТИ Для исследования частотной характеристики подадим на вход синусоидальную последовательность x(t) = Xosincotj,. Если система линейна, на выходе также возникнет синусоида. Отнощение амплитуд, как и в аналоговых фильтрах, равно значению передаточной функции р = jco. Линейность цифрового фильтра следует из линейности дифференциального уравнения. Таким образом, согласно формуле (22.8), фильтр на рис. 22.6 линеен. Передаточная функция может быть получена, как и в случае аналогового фильтра, расчетом с использованием комплексных переменных. Найдем частотную характеристику элемента задержки. Для гармонического входного сигнала x(f,) = хое получается гармонический выходной сигнал y(t,) = XoeV-i) = хое .- и с учетом j(o = р передаточная функция имеет вид А{р) = 1-е -рТа (22.9) Эта функция периодическая с периодом Год = 2я/7 = 2я/ Здесь / -тактовая часто- та. Введем обозначение (22.10) и получим из формулы (22.9) передаточную функцию в виде 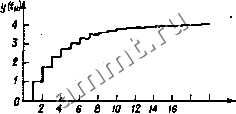 18 го м Рис. 22.7. Переходная характеристика цифрового фильтра, показанного на рис. 22.6, для Со = = -0,75 при переходе входного сигнала из О в 1. Aiz) = 2 (22.11) В гл. 13 уже отмечалось, что передаточная функция А (р), связывающая выходной и входной сигналы, имеющие произвольную зависимость от времени, с помощью преобразования Лапласа может быть представлена в виде L{y(t)} = A(p)-L{x{t)}. (22.12) Это соотношение справедливо и для цифровых систем. Для числовых последовательностей его можно упростить с помошью преобразования передаточной функции (22.11): Z{y{0} = A{z).Z{x{t,)}. (22.13) Здесь Z {х (д} = X (z) = £ X (g z-(22.14) ц = 0 есть Z-преобразование входной последовательности. Выходная последовательность получается с помошью соответствующего обратного преобразования [22.2]. Функция A(z) называется цифровой передаточной функцией. Теперь, используя выражение (22.11), можно непосредственно определить передаточную функцию цифрового фильтра, показанного на рис. 22.6. Из соотношения Y(z)[X{z)-CoY(zy]z- получаем Л(2)= l/(Co + z). (22.15) Для определения частотной характеристики а (/оэ) подставим в формулу (22.15) z = = е ; в результате получим А Ои) = Со -l-cosco7i +jsm(i>T, (22.16) Функция является периодической с периодом 2л/,. Это свойство-общее для всех цифровых фильтров. Для модуля частотной характеристики имеем \Ат\ - у {Со + COS со г/ -t- sincor. График этой функции приведен на рис. 22.8. Видно, что эта амплитудно-ча- 2я Зп стотная характеристика в области О соГ < л, т.е. О V/e. имеет вид характеристики фильтра нижних частот, как мы и ожидали, исходя из переходной характеристики на рис. 22.7. На основании теоремы о дискретизации для дискретной системы задержки, работающей на частоте частота синусоидальной последовательности {х(д} выбирается не больше чем jJa- В области частот / > Vifa амплитудно-частотная характеристика устройства уже не имеет вида, присущего фильтру. Если все же желательно использовать такое устройство, необходимо заменить цифровой элемент задержки аналоговым элементом задержки (например, линией задержки или фазовым фильтром). 22.3. БИЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ Желательно, чтобы цифровые фильтры имели описанную в гл. 13 оптимизированную передаточную функцию аналогового фильтра. Однако, как отмечалось в предыдущем разделе, это невозможно, поскольку цифровой фильтр в отличие от аналогового в диапазоне О < / < оо обладает периодической передаточной характеристикой. Однако используемая полоса частот ограничена соотношением О < / /гЛ. поэтому поставленную задачу в дальнейшем можно видоизменить таким образом, чтобы частотная характеристика сохраняла желаемый вид лишь до значения /гЛ и периодически не повторялась в области /> Для этого можно модифицировать амплитудно-частотную характеристику аналогового фильтра посредством преобразования оси частот, подобно тому как это было сделано при преобразовании фильтра нижних частот в полосовой фильтр, а именно таким образом, чтобы область Рис. 22.8. Амплитудно-частотная характе- ристика цифрового фильтра при Со = Uila = -0,75.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |