
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
|
Читальный зал --> Полупроводниковая схемотехнология торым отличительным свойствам полученных коэффициентов можно непосредственно, как и в случае аналоговых фильтров, найти способ построения фильтра. Используя выражения (22.25), получаем следующие соотношения: для фильтра нижних частот А(Р) Со + с,Р ► /1(2) = Do 44. (22.29) Со + Z А{Р) ДЛЯ фильтра верхних частот d,P Со + С,Р -4(z) = Оо--- (22.30) Фильтры нижних частот характеризуются, таким образом, соотношением = Do, а для фильтров верхних частот = -Dq. Отсюда понятно, почему схема, приведенная на рис. 22.6, не является истинным фильтром нижних частот, а обладает лишь похожей характеристикой: коэффициент в формуле (22.28) не равен Dq. Это означает, что коэффициент соответствующего аналогового фильтра не равен нулю. Поэтому затухание на высоких частотах остается конечным. влять каскадирование фильтров первого и второго порядка. Необходимая для этого факторизованная форма передаточной функции легко может бьггь получена подстановкой коэффициентов, приведенных на рис. 13.14, в формулы (22.26). Передаточная функция A(z) блока фильтрации на рис. 22.13 получена тем же способом, что и для фильтра первого порядка. Анализируя схему на рис. 22.13, можно записать Y = DiX + z X [DjX -CJ+ z-{DoX - Со У)]. Отсюда следует Y(z) A(z) Xiz) °;;:-\(22.з1) Со +Cz + С помощью этой схемы можно реализовать любую искомую передаточную функцию фильтра второго порядка. Теперь, как и в случае фильтров первого порядка, рассмотрим некоторые специфические свойства коэффициентов. Применяя формулы пересчета (22.26) для различных способов фильтрации, можно получить следующие выражения: для фильтра нижних частот 22.4.2. СТРУКТУРА ЦИФРОВЫХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА Если к схеме на рис. 22.12 прибавить звено задержки, то получится фильтр второго порядка, который представлен на рис. 22.13. Существует, кроме того, возможность дальнейшего наращивания схемы [22.2], которую здесь, однако, мы не будем рассматривать подробно. Фильтр более высокого порядка может быть реализован добавлением следующего элемента задержки. Наиболее просто осущест- А{Р) = Со + CiP + сР I +2z + z = ц> Co + Qz + z (22.32) для фильтра верхних частот А{Р) = Со + CiP + СР l-2z + z >A(z) Со -I- CiZ -I- z (22.33) 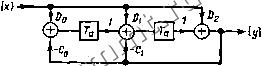 Рис. 22.13. Цифровой фильтр второго порядка. для полосового фильтра d,P А(Р) Со + сР + сР 1 -г A{z) Со + Qz -I- Z (22.34) Выбор параметров схемы проиллюстрируем числовым примером. Рассмотрим фильтр Чебышева нижних частот второго порядка с неравномерностью 0,5 дБ и затуханием 3 дБ на частоте среза fg= 100 Гц. Аналоговый сигнал зани.мает полосу 3,4 кГц, а частота выборки / = ,= 10 кГц. Отсюда получается норгш1ро-ванная частота выборки =/Л = 10 кГц/100 Гц = 100. Используя формулу (22.21), определяем нормированный коэффициент / = ctg- = 31,82. Из табл. 13.6 получаем непрерывную пере даточную функцию А(Р) = 1 + 1,3614 Р + 1,3827 Сравнивая найденное выражение с формулой (22.23), определяем значения коэффициентов do =1, = 2 = О, Со = 1, с, = 1,3614, С2 = 1,3827. Подстановка этих значений в формулы (22.26) дает Do = 6,923 Ю-*, Со = 0,9400, Cl = - 1,937. Из формулы (22.32) находим цифровую передаточную характеристику I +2z + A(z) = 6,923 10- 0,9400 - l,937z + z которая может быть реализована по схеме, приведенной на рис. 22.13. Отношение частоты выборки к частоте среза для выбранных параметров составляет 100. Частота среза пропорциональна частоте выборки. Следовательно, частотой среза можно управлять с помощью частоты выборки. Это особенность всех цифровых фильтров. В качестве второго примера рассмо- трим полосовой фильтр. Частота выборки, как и в предыдущем примере, составляет 10 кГц. Резонансная частота /, = 1 кГц. Следовательно, = = 10. При добротности 10 непрерывная передаточная характеристика определяется из формулы (13.24): Л(Р) = 0,1 Р 1 + 0,1Р + Отсюда с учетом формулы (22.26) при / = = ctg- = 3,078 находим цифровую перелоя даточную функцию A{z)= -2,855-10-- 0,9429 - l,572z -I- z При добротности 100 имеем 1 -2 A(z)= -2,930-10-з. 0,9941 - l,613z + z Рассмотрим теперь случай g = 10 и fi = = 100. При этом получается A(z) = -3,130-10- 0,9937 - l,990z -I- z С возрастанием добротности и частоты выборки коэффициент Do всегда уменьшается, тогда как Со -> 1 и С, - - 2. Параметры фильтра очень близки к 1 и - 2 соответственно. Это усиливает требования к точности коэффициентов, т.е. нужна большая длина слова в фильтре. Чтобы ограничить аппаратурные затраты, необходимо выбирать частоту выборки по возможности малой. 22.4.3. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ При разработке цифровых фильтров основные затраты связанны с реализацией элементов задания масштабных коэффициентов, которые обеспечивают умножение сигнала на заданный коэффициент. Длина слова в фильтре должна быть выбрана большей, чем входной или выходной сигналы, на число разрядов коэффициентов, с тем чтобы при умножении не произошло существенной потери информации. В противном случае характеристика фильтра будет зависеть от амплитуды. Это ведет к искажениям. Требования к точности умножителя для коэффициентов, стоящих в знаменателе, тем больше, чем ближе Со к 1 и к - 2. В данном случае можно, однако, ослабить эти требования посредством следующего преобразования: СоУ = tl - Со)у = у - Соу. Здесь Со = 1 - Со и, очевидно, меньше 1. Этот коэффициент имеет значительно меньше значащих разрядов, чем Со. Чаще всего для фильтра первого порядка достаточно 4 разряда, а для фильтра второго порядка-8 разрядов. Дополнительные аппаратурные затраты для схемы вычитания малы по сравнению с экономией в умножителе. Подобным же образом можно представить коэффициент С у. Су = (-2+Ci)y = -2у + С\у, где Cl = 2 + Cl. Простой пример реализации цифрового фильтра В качестве примера рассмотрим фильтр верхних частот первого порядка. Его частота среза должна составлять 100 Гц, ширина полосы входного сигнала 3,4 кГц. Выберем = 10 кГц, т.е. П = 100. Из выражения А{Р) = Р/(1 + Р) с учетом формулы (22.25) получим 1 - 2 А(2)= -0,9695- - 0,9695 - 0,9391 + 2 1 - 2 (- 1 Н- 0,0609) -I- 2 Для того чтобы можно было оперировать в двоичной системе, преобразуем Со в двоичную дробь: (0,0609)io = (0,000011111001...)2. Это число близко к 2 * = 0,0625. Можно значительно уменьшить затраты на вычисление произведения СоУ, если Со будет точно равняться целочисленной степени двух, в рассматриваемом случае Cq = 2~*. Тогда умножение выполняется просто сдвигом у на четыре двоичных разряда. Из анализа формул (22.25) можно заключить, что поставленное условие может быть выполнено путем незначительного изменения нормировочного коэффиццента /, т.е. изменением П; из выражения Со = следует -1 -Ь 2-* г = .,Д * = 31, т.е. П. = 97,423. Это означает, что при частоте выборки 10 кГц частота среза fg возрастает со 100 до 102,6 Гц. Коэффициенту Do также придаем приближенное значение Z)o = - 1 + 2 * = -0,9687.... Так как этот параметр влияет только на коэффициент усиления, для дальнейшего упрощения схемы будем считать его равным - 1, т.е. коэффициент усиления на высоких частотах стремится к значению (1 + 1)11 = 1,0323. После этих упрощений получаем блок-схему, приведенную на рис. 22.14, с цифровой передаточной характеристикой A(z) -1 Н- Z (-1 -Н 2-*)4-z Схемотехническая реализация с 4-разрядным входным кодом показана на рис. 22.15. Для того чтобы иметь возможность оперировать и с положительными, и с отрицательными числами, используется {х1- -Со = /-2-* Рис. 22.14. Цифровой фильтр верхних частот первого порядка. Частота среза /, =/,/П, =/,/97,42. Коэффициент усиления А = 1 -1-(1/0 = 1,032.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |