Читальный зал -->  Полупроводниковая схемотехнология 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 [ 31 ] 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168

вить УвгХО. При этом длительность выходного импульса одновибратора составит

tgX RC In 2x0,7RC.

(8.2)

По истечении этого времени транзистор Т2 откроется и схема опрокинется в исходное состояние. Вышеизложенное справедливо для случая, когда длительность управляющего импульса на входе схемы меньше, чем величина t. Временная диаграмма напряжений в различных точках схемы одно-вибратора приведена на рис. 8.15.

*Д-г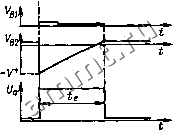

Рис. 8.15. Временная диаграмма работы одно-вибратора.

8.4. НЕСТАБИЛЬНАЯ РЕЛАКСАЦИОННАЯ СХЕМА

Если в схеме одновибратора на рис. 8.16 второй резистор обратной связи также заменить конденсатором, то оба состояния схемы будут стабильны, каждое

Vet Ув2

1 1

Рис 8.16. Мультивибратор (длительности импульсов: ti = RiCiln2; = КСЫг).

в течение ограниченного интервала времени. Таким образом, если схему однажды возбудить, она будет непрерывно

опрокидываться из одного состояния в другое. Ее обычно называют мультивибратором. Величины длительности каждого из двух состояний мультивибратора определяются из формулы (8.2). Они составляют

fi = /?iCiln2, tj = R2<2ln2.

Если необходимо с помошью электрического сигнала управлять и t, то резисторы и R2 можно заменить управляемыми стабилизаторами тока. Временная диаграмма напряжений в различных точках мультивибратора приведена на рис. 8.17.

:y V 1/

Рис. 8.17. Временная диаграмма работы мультивибратора.

На частотах ниже 100 Гц конденсаторы в схеме мультивибратора должны иметь слишком большую емкость. На частотах свьпие 10 кГц становится заметным вредное влияние инерционности транзисторов. Все это указывает на то, что большого практического значения схема, приведенная на рис. 8.16, не имеет. На низких частотах преимущественно используют прецизионные схемы на базе компараторов, рассмотренные в разд. 18.5.1, а на высоких частотах-эмиттерно-связанные мультивибраторы, рассмотренные в разд. 18.5.2.

9. Базовые логические схемы

На первый взгляд цифровые устройства кажутся относительно сложными. Однако они основаны на принципе многократного повторения относительно простых базовых логических схем. Связи между этими схемами строятся на основе чисто формальных методов. Инструментом такого построения служит булева алгебра, которая применительно к цифровой технике называется также алгеброй логики. Основные понятия алгебры логики приводятся в последующих разделах.

9.1. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ

В отличие от переменной в обычной алгебре логическая переменная имеет только

Коммутативный закон:

XjXj = XjXi (9.1а)

Ассоциативный закон:

Х1(х2Хз) = (xiX2)x3 (9.2а)

Дистрибутивный закон:

Xi (xj + Хз) = XiXj + Х1Х3 (9.3а)

два значения, которые обычно называются логическим нулем и логической единицей. В качестве обозначений используются О и 1 или просто О и 1. В дальнейшем мы будем придерживаться последнего обозначения. Не следует опасаться спутать эти символы с числами О и 1, так как в каждом конкретном случае бывает ясно, относится ли данная запись к числу или к логическому значению.

Существуют три основные операции между логическими переменными: конъюнкция (логическое умножение), дизъюнкция (логическое сложение) и инверсия (логическое отрицание). По аналогии с алгеброй чисел в алгебре логики используются следующие обозначения операций.

Конъюнкция: у = Xj л х = Xj -Xj =

= XiX2.

Дизъюнкция: у = xs/x = Xi + Xj. Инверсия: у = x.

Применительно к логическим операциям существуют теоремы:

Xi + Х2 = Х2 + Xi

(9.16)

xi + (Х2 + Хз) = (Xj -t- xj) + Хз (9.26)

Xi + X2X3 = (Xi + X2)(xi + X3) (9.36)

Правило склеивания:

Xi (Xi + X2) = Xi

Правило повторения:

XX = X

Правило отрицания:

XX = О

Правило двойного отрицания:

Щ = х Теорема де Моргана:

XjX2 - 1 4 Х2

Операции с О и 1:

х-1 = X хО = О 0=1

(9.4а) (9.5а) (9.6а)

(9.7)

(9.8а)

(9.9а) (9.10а) (9.11а)

Х1Х2 - Xj

X + X = X

X Ч- X = 1

Xj -Ь Х2 - Х1Х2

X + о = X х + 1 = 1 1 = О

(9.46)

(9.56)

(9.66)

(9.86)

(9.96) (9.106) (9.116)

Многие из этах теорем уже известны из алгебры чисел. Однако теоремы (9.36), (9.4 а, б), (9.5 а, б) и (9.10 6) для чисел несправедливы; кроме того, понятие инверсия для чисел вообще не определено. Выражения типа 2х и в алгебре логики не встречаются в силу правила повторения.

Сравнивая левые и правые уравнения, следует обратить внимание на содержащийся в них дуализм: если в каком-нибудь тождестве поменять местами конъюнкцию с дизъюнкцией и О с 1, то при этом также получится тождество.

С помощью выражений (9.9)-(9.11) можно вычислить результаты конъюнкции и дизъюнкции для всех возможных значений переменных х, и Xj. В табл. 9.1 и 9.2

Таблица 9.1

Таблица истинности для логического умножения

(конъюнкции) у = XiX2

Таблица 9.2

Таблица истинности для логического сложения (дизъюнкции) у = Xi + Х2

представлены функции соответственно для конъюнкции и дизъюнкции.

Из табл. 9.1 следует, что у только тогда равен 1, когда х, и Хг равны 1. На этом основании операция конъюнкции называется также функцией И. При дизъюнкции двух переменных у равен 1 тогда, когда Xi или Х2 равны 1. Поэтому операцию дизъюнкции называют также функцией ИЛИ. Обе эта функции можно распространить на сколь угодно больщое число переменных.

Возникает вопрос: как можно представить логические функции с помощью электрических переключающих схем? Так как логические переменные могут иметь толь-

ко ,ва дискретных значения, то следует обратить внимание на схемы, которые могут находиться в двух легко различимых рабочих состояниях. Простейпшм способом реализации логической переменной является ключ, изображенный на рис. 9.1.

Рис. 9.1. Представление логической переменной в ввде ключа.

Можно условиться, что разомкнутый ключ эквивалентен логическому нулю, а замкнутый-логической единице. Таким образом, ключ реализует переменную х, если он замкнут при х = 1, и переменную х, если он разомкнут при х = 1.

Рассмотрим сначала, какая логическая функция будет реализована, если два ключа Xi и соединить последовательно, как показано на рис. 9.2. Значение зависимой

Xj Хг о-ж- *--о

Рис. 9.2. Схема И.

переменной у характеризуется тем, будет ли замкнута или разомкнута составная коммутируемая цепь, расположенная между входными клеммами. Очевидно, что рассматриваемая цепь будет замкнута только тогда, когда х, и Xj замкнуты, т. е. равны единице. Таким образом, последовательное включение ключей реализует функцию И. Функция ИЛИ может быть получена, если ключи включить параллельно.

С помощью такой схемной логики можно наглядно показать справедливость ранее приведенных теорем. Рассмотрим это на примере правила повторения. На рис. 9.3 показана реализация обеих частей выражения (9.5 а) с помощью коммутируемой цепи. Легко заметить, что рассматриваемое тождество выполняется, поскольку два включенных последовательно ключа, замыкание и размыкание которых происходит одновременно, воздействуют на внехпние цепи как один такой ключ.

Другой возможностью представления логических переменных является электрическое напряжение, имеющее два различных уровня: высокий и низкий, которое было рассмотрено в разд. 8.1. Этим уров-

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 [ 31 ] 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.