
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
|
Читальный зал --> Полупроводниковая схемотехнология
Рис. 13.22. Иллюстрация преобразования нижних частот в полосу частот. передачи уменьшается на 3 дБ: Пмакс/мин = + 4 ± ДП- 13.6.1. полосовой поряд1а ФИЛЬТР ВТОРОГО Простейший полосовой фильтр можно получить, применив преобразование (13.21) к передаточной функции фильтра нижних частот первого порядка: А (Р) = Ло/(1 + Р). При этом передаточная функция полосового фильтра будет иметь второй порядок: А(Р): [Р + (1/Р)] оДПР 1 + ДПР + (13.22) Основными характеристиками такого фильтра являются коэффициент; передачи А, на резонансной частоте и добротность Q. Исходя из свойств рассмотренного преобразования, можно заключить, что А, -= Aq. это легко подтвердить, положив в формуле (13.22) £1=1, т.е. P=j. Поскольку при этом Аг имеет действительное значение, фазовый сдвиг на резонансной частоте полосового фильтра будет равен нулю. По аналогии с колебательным контуром определим добротность полосового фильтра как отношение резонансной ча- стоты /, к ширине полосы В. Отсюда следует, что . е=л/В=/Жмакс-/м ) = = 1/(П , - П ) = 1/АП. (13.23) Подставив выражение для добротности в соотношение (13.22), получим передаточную функцию полосового фильтра А(Р) = (AJQ)P 1 + -Р + Р Q (13.24) Это выражение дает возможность определить основные параметры полосового фильтра второго порядка непосредственно из его передаточной функции. Подставив в выражение (13.24) Р = jQ, получим амплитудную и фазовую частотные характеристики: А = ф = arctg 6(1 -n ) n (13.24a) (13.246) Логарифмические амплитудно- и фазово-частотные характеристики полосовых фильтров, добротность которых равна 1 и 10, изображены на рис. 13.23. Рис. 13.23. Амплитудно- и фа-зово-частотные характеристики полосовых фильтров второго порядка с добротностью Q = 1 I е = 10.
0,1 0,2 Рис. 13.24. Амплитудно-I фазово-частотные характеристики полосовых фильтров с Afi = 1. -фш1ьтр Баттерворта четвертого по-щка;2-фильтр Чебышева четвертого Kfima с неравномерностью 0,5 дБ; J-полосовой филь1р второго порядка.
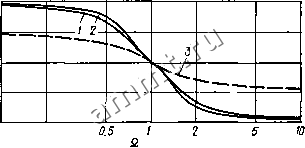 0,1 0,2 13.6.2. ПОЛОСОВОЙ ФИЛЬТР ЧЕТВЕРТОГО ПОРЯДКА В полосовых фильтрах второго порядка амплитудно-частотная характеристика тем острее, чем больше величина их добротно-сга. Существуют, однако, случаи, когда в окрестности резонансной, частоты необходимо получить возможно более плоскую характеристику с крутым спадом за полосой прозрачности. Такая задача оптимизации может быть решена путем преобразования фильтров нижних частот более высокого порядка в , полосовые. При этом предоставляется возможность кроме ширины полосы AQ задать и желаемый вид частотной характеристики. Особое значение имеет применение рассмотренного ранее преобразования к фильтрам нижних частот второго порядка. Оно приводит к описанию полосовых фильтров четвертого порядка, которые ниже будут рассмотрены более подробно. Подставив (13.21) н уравнение фильтра нижних частот второго порядка (13.17), получим следующую передаточную функцию четвертого порядка; bi J (13.25) Отсюда видно, что амплитудно-частотная характеристика фильтра на нижних и верхних частотах стремится к асимптотам ± 12 дБ на октаву. На средней частоте П = 1 коэффициент передачи фильтра имеет действительное значение = Aq. На рис. 13.24 приведены амплитудно- и фазово-частотные характеристики при нормированном значении АП = 1 для полосового фильтра Баттерворта и полосового фильтра Чебышева с неравномерностью характеристики, равной 0,5 дБ. Для сравнения представлены частотные характеристики полосового фильтра второго порядка с такой же полосой пропускания. Как и в случае фильтров нижних частот, для облегчения реализации разложим знаменатель передаточной функции (13.25) на множители. Из соображений симметрии выберем следующее упрощенное представление: (13.26) Перемножив сомножители в знаменателе и приравняв результат знаменателю передаточной функции (13.25), получим уравчение для определения параметра сх: .-2-i = 0. Это уравнение в каждом конкретном случае может быть легко решено численно с помощью калькулятора. Определив параметр сх, можно вычислить добротность полюсов звеньев фильтра б,-: Si = (1 + cx)bi/aAnai. (13.28) В зависимости от того, как будет разложен числитель передаточной функции полосового фильтра, мы получим два способа его реализации. Если представить числитель в виде произведения постоянного множителя и множителя, содержащего Р, то это будет соответствовать последовательному соединению фильтра верхних чдстот и фильтра нижних частот. Такой способ реализации применяется в основном при достаточно широкой полосе пропускания фильтра AQ. При узкополосном фильтре (ДП < 1) лучше применять последовательное соединение двух полосовых фильтров второго порядка, которые имеют небольшой сдвиг частотных характеристик. Такой способ называют расстройкой контуров . Для расчета полосового фильтра представим числитель выражения (13.26) в виде произведения двух сомножителей, содержащих Р: 1+ + {аР) Q, Qi (13.29) Приравняв коэффициенты выражений (13.26) и (13.24), получим формулы для расчета параметров звеньев фильтра (табл. 13.8):
(13.27) Здесь/ -средняя частота результирующего полосового фильтра, а коэффициент передачи на этой частоте. Значения параметров сх и Q; могут быть получены из соотношений (13.27) и (13.28).
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |