
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
|
Читальный зал --> Полупроводниковая схемотехнология на множители. Если среди корней полино-ч ма есть комплексные, то рассмотренное ранее представление полинома (13.2) не может быть использовано. В этом случае следует записать его в виде произведения сомножителей второго порядка: Л(Р) - (1 -I- а,Р + i,P)(l -I- а,Р + frP)- (13.4) где а,- и Ь, - положительные действительные коэффициенты. Для нечетных порядков полинома коэффициент bj равен нулю. Параметры фильтра могут быть оптимизированы по различным критериям. Для удовлетворения каждому из выбранных критериев оптимизации коэффициенты О; и Ь, передаточной функции А(Р) должны иметь строго определенные значения. Как мы увидим в дальнейшем, корни полинома могут иметь сопряженные комплексные значения, что приводит к невозможности реализации такого фильтра с помощью пассивных ЯС-цепей. Для реализации фильтров с сопряженными комплексными корнями могут быть использованы LRC-фильтры. Для высоких частот получение необходимых индуктивностей не представляет затруднений. Однако для низких частот нужны большие индуктивности, которые сложны в изготовлении и обладают плохими электрическими характеристиками. Применения индуктивностей для фильтров в низкочастотном диапазоне можно избежать, используя ЯС-схемы с активными элементами (например, операционными усилителями). Такие схемы далее будем называть активными фильтрами. Рассмотрим теперь различные способы задания оптимальных характеристик фильтров нижних частот, схемная реализация которых будет описана в следующих разделах. Амплитудно-частотная характеристика фильтра Баттерворта имеет довольно длинный горизонтальный участок и резко спадает за частотой среза. Переходная характеристика такого фильтра при ступен- 10 О -10 -60 10 -30 -40 -50 -SO 0.01 0,03 Рис. 13.2. Амплитудно-частотные характеристики фильтров четвертого (а) и десятого (б) порядков. J-фильтр с критическим затум-нием; 2-фильтр Бесселя; i-фильтр Баттерворта; -филыр Чебышева с неравномерностью ЗдБ. 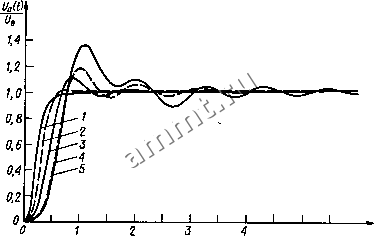 5 t/r Рис. 13.3. Переходные характеристики фильтров нижних частот четвертого порядка при ступенчатом входном сигнале. J-фильтр с критическим затуханием; 2-х)ИЛЬтр Бесселя; 3-фильтр Баттерворта; 4-фильтр Чебышева с неравномерностью 0,5 дБ; )-фш1ьтр Чебышева с неравномерностью 3 дБ. чатом входном сигнале имеет колебательный характер. С увеличением порядка фильтра колебания усиливаются. Характеристика фильтра Чебышева спадает более круто за частотой среза. В полосе пропускания она, однако, не монотонна, а имеет волнообразный характер с постоянной амплитудой. При заданном порядке фильтра более резкому спаду амплитудно-частотной характеристики за частотой среза соответствует большая неравномерность в полосе пропускания. Колебания переходного процесса при ступенчатом входном воздействии сильнее, чем у фильтра Баттерворта. Фильтр Бесселя обладает оптимальной переходной характеристикой. Причиной этого является пропорциональность фазового сдвига выходного сигнала фильтра частоте входного сигнала. В общем случае спад амплитудной характеристики фильтра Еесселя оказывается более пологим по сравнению с фильтрами Чебышева и Баттерворта. - На рис: 13.2 показаны амплитудно-час-тогаые характеристики четырех рассмотренных фильтров нижних частот четвертого и десятого порядка. Можно заметить, что характеристика фильтра Чебышева шеет наиболее крутой спад для частот входного сигнала, превышающих частоту среза, но заметную неравномерность в полосе пропускания. При увеличении равномерности амплитудной характеристики фильтр Чебышева переходит в фильтр Баттерворта [13.1]. Переходные характеристики этих фильтров имеют большую амплитуду колебаний при ступенчатом входном сигнале. Это хорошо видно из рис. 13.3. Переходный процесс для фильтра Бесселя практически не имеет колебаний. Несмотря на менее удовлетворительные амплитудно-частотные характеристики фильтра Бесселя, он обеспечивает весьма высокое качество отработки ступенчатого входного сигнала. Пассивный ЯС-фильтр нижних частот не имеет перерегулирования, однако обладает значительно худшей амплитудно-частотной характеристикой по сравнению с фильтром Бесселя и несколько уступает ему в отношении качества отработки входного ступенчатого сигнала. В табл. 13.1 приведены значения времени нарастания и задержки выходного сигнала, а также относительного перерегулирования для фильтров нижних частот различного типа. Время нарастания определяет интервал, за который выходной сигнал возрастает от 10 до 90% своего установившегося значения. Время задержки соответствует интервалу, в течение которого
Фильтр Чебышева с неравномерностью 1 дБ Время нарастания tJTg 0,334 0,421 0,486 0,537 0,582 Время задержки tJTg 0,260 0,572 0,893 1,215 1,540 Относительная величина перерегулирования, % 14,6 21,6 24,9 . 26,6 27,8 Фильтр Чебышева ностъю 2 дБ с неравномер-
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||